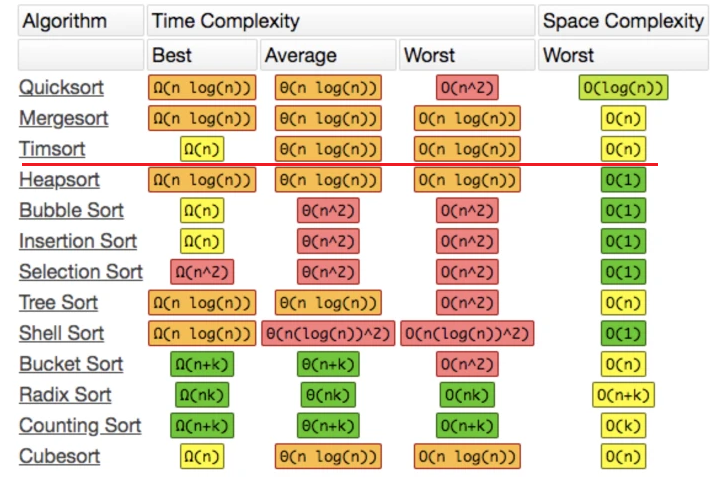
Timsort 算法是一个以人名命名的，工业级、稳定型排序算法。Python 中内置sorted函数和各类中的sort方法都是用的 Timesort。

性能

最好的情况下可以达到 O(n)，最差情况下也不过 O(n log(n))，这属于是排序算法中最好的情况了。和堆排序的优劣在于，最好情况下堆排序为O(n log(n))（比timsort慢）,空间上堆排为 O(1)，timsort为 O(n)。

解析

Timsort的大致步骤可以分为3步：

1. 将数据按照单调递增或单调递减分割为多个独立的切片，每个切片称作一个run，并将单调递减的 run 翻转。
2. 定义一个长度阈值，将长度低于这个阈值的 run 与相邻的 run 合并，以提高后续归并的效率。
3. 将所有的 run 依次压入栈中，并使得在压入栈的过程中，三个连续的 run [X, Y, Z] 始终满足 len(X) + len(Y) < len(Z) 和 len(X) < len(Y) 的条件。如果不满足以上条件，则将 Y run 与 X, Z 中较短的 run 通过归并排序合并。

以上三个步骤为 timsort 算法的核心思想，每个步骤的实现会因人而异，总体的核心代码如下：

MIN_SORT_LEN = 32  # 可以根据数据的规模规定长度阈值

def my_timsort(data):

    # 步骤1：
    # 将数据按照单调递增或单调递减分割为多个数据切片，每个切片称作run
    # 其中，单调递减的切片会被反转为单调递增的
    runs = splite_runs(data)

    # 步骤2：
    # 将过短的run跟相邻的run通过插入排序合并，
    # 需要定义一个数值来判定run是否过短
    runs = merge_short_runs(runs, MIN_SORT_LEN)

    # 步骤3：
    # 将所有的run，依次压入栈中，
    # 使得栈中的任意三个连续的run [X, Y, Z] 满足：
    # 1. len(X) + len(Y) < len(Z)
    # 2. len(X) < len(Y)
    # 如果不满足以上条件，则 Y 与 X, Z 中较小的一个run通过归并排序合并
    sorted_data = merge_runs(runs)

    return sorted_data

分割 run

将数据按照单调递增或单调递减分割为多个独立的切片，每个切片称作一个run，并将单调递减的 run 翻转。

def splite_runs(data):
    """
    分割 run
    将数据按照单调递增或单调递减分割为多个独立的切片，
    每个切片称作一个run，并将单调递减的 run 翻转。
    """
    runs = []
    curr_run = []
    need_reverse = False
    for i in data:

        if len(curr_run) < 2:
            curr_run.append(i)
            continue
        if len(curr_run) == 2:
            need_reverse = True if curr_run[0] > curr_run[1] else False
        
        # start_a_new_run = False
        if not need_reverse and i < curr_run[-1]:
            # 单调递增时遇到了比最后一个元素小的元素
            pass
        elif need_reverse and i > curr_run[-1]:
            # 单调递减时遇到了比最后一个元素大的元素
            pass
        else:
            curr_run.append(i)
            continue

        # 开始下一个 run
        if need_reverse:
            curr_run.reverse()
        runs.append(curr_run)
        curr_run = [i]
    
    if curr_run:
        runs.append(curr_run)
    
    return runs

合并短 run

定义一个长度阈值，将长度低于这个阈值的 run 与相邻的 run 合并，以提高后续归并的效率。

def my_bisect_pos(data, x):
    """二分查找"""
    if not data:
        return 0
    if len(data) == 1:
        if data[0] > x:
            return 0
        else:
            return 1

    mid = round(len(data)/2)
    if data[mid] < x:
        return mid + my_bisect_pos(data[mid:], x)
    elif x < data[mid]:
        return my_bisect_pos(data[:mid], x)
    else:
        return mid


def my_insertion_sort(data):
    """插入排序"""
    
    p = 1
    new_data = [data[0]]
    while p < len(data):
        new_pos = my_bisect_pos(new_data, data[p])
        new_data = new_data[:new_pos] + [data[p]] + new_data[new_pos:]

        p += 1
    
    return data


def merge_short_runs(runs, min_run_len):
    """
    合并短 run
    定义一个长度阈值，将长度低于这个阈值的 run 与相邻的 run 合并，
    以提高后续归并的效率。
    """
    sorted_runs = []
    curr_run = []
    for run in runs:
        if len(curr_run) >= min_run_len:
            sorted_runs.append(my_insertion_sort(curr_run))
            curr_run = run
        else:
            curr_run.extend(run)
    sorted_runs.append(my_insertion_sort(curr_run))
    return sorted_runs

按规则归并 run

将所有的 run 依次压入栈中，并使得在压入栈的过程中，三个连续的 run [X, Y, Z] 始终满足 len(X) + len(Y) < len(Z) 和 len(X) < len(Y) 的条件。如果不满足以上条件，则将 Y run 与 X, Z 中较短的 run 通过归并排序合并。

def merge_run(run_a, run_b):
    """归并排序"""
    new_run = []
    p_a = p_b = 0
    while p_a < len(run_a) and p_b < len(run_b):
        if run_a[p_a] <= run_b[p_b]:
            new_run.append(run_a[p_a])
            p_a += 1
        else:
            new_run.append(run_b[p_b])
            p_b += 1
    if p_a < len(run_a):
        new_run.extend(run_a[p_a:])
    if p_b < len(run_b):
        new_run.extend(run_b[p_b:])
    return new_run


def merge_runs(runs):
    """
    按规则归并 run
    将所有的run，依次压入栈中，
    使得栈中的任意三个连续的run [X, Y, Z] 满足：
    1. len(X) + len(Y) < len(Z)
    2. len(X) < len(Y)
    如果不满足以上条件，则 Y 与 X, Z 中较小的一个run通过归并排序合并
    """
    run_stack = []
    for run in runs:
        run_stack.append(run)
        while len(run_stack) >= 3:

            Z = run_stack.pop()
            Y = run_stack.pop()
            X = run_stack.pop()

            if len(X) + len(Y) < len(Z) and len(X) < len(Y):
                run_stack.append(X)
                run_stack.append(Y)
                run_stack.append(Z)
                break

            else:
                if len(Z) < len(X):
                    run_stack.append(X)
                    run_stack.append(merge_run(Y, Z))
                else:
                    run_stack.append(merge_run(X, Y))
                    run_stack.append(Z)
    sorted_data = []
    for run in run_stack:
        sorted_data = merge_run(sorted_data, run)
    return sorted_data